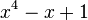Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Verhalten nahe 0: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 27: | Zeile 27: | ||
'''a)''' | '''a)''' | ||
<math>x^4-x+1</math> | <math>x^4-x+1</math> | ||
| − | |||
'''b)''' | '''b)''' | ||
| − | <popup Name="Lösung">a) [[Datei:Geogebra7.png|miniatur]]</popup> | + | '''c)''' |
| + | |||
| + | <popup Name="Lösung">a) [[Datei:Geogebra7.png|miniatur|lins]]</popup> | ||
}} | }} | ||
Version vom 12. November 2019, 11:59 Uhr
|
|
|
Gegeben ist die Funktion f mit |
|
Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0. a)
b)
c)
|
|
Skizziere folgende Graphen. Achte dabei auf das Verhalten nahe Null und gegen Unendlich. a)
b) c) |
 hat als höchsten Exponenten 4, verhält sich also gegen Unendlich wie
hat als höchsten Exponenten 4, verhält sich also gegen Unendlich wie  . Also geht sie für x gegen - Unendlich gegen + Unendlich und für x gegen + Unendlich auch gegen + Unendlich.
Die Funktion verhält sich nahe 0 wie der x-Wert mit dem kleinsten Exponenten und dem absoluten Glied, also wie
. Also geht sie für x gegen - Unendlich gegen + Unendlich und für x gegen + Unendlich auch gegen + Unendlich.
Die Funktion verhält sich nahe 0 wie der x-Wert mit dem kleinsten Exponenten und dem absoluten Glied, also wie 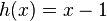 . Damit ist es nahe 0 annähernd eine Gerade, die die Steigung 1 und den y-Achsenabschnitt -1 hat.
. Damit ist es nahe 0 annähernd eine Gerade, die die Steigung 1 und den y-Achsenabschnitt -1 hat. . Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0.
. Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0.

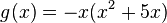

 , also x--> -∞ = ∞
, also x--> -∞ = ∞